当前的位置： 捷杰建站   开发技术

LRU缓存替换策略及C#实现方法是什么

开发技术 作者：iii 2024-05-08 14:30:01
这篇“LRU缓存替换策略及C#实现方法是什么”文章的知识点大部分人都不太理解，所以小编给大家总结了以下内容，内容详细，步骤清晰，具有一定的借鉴价值，希望大...

这篇“LRU缓存替换策略及C#实现方法是什么”文章的知识点大部分人都不太理解，所以小编给大家总结了以下内容，内容详细，步骤清晰，具有一定的借鉴价值，希望大家阅读完这篇文章能有所收获，下面我们一起来看看这篇“LRU缓存替换策略及C#实现方法是什么”文章吧。

LRU缓存替换策略

缓存是一种非常常见的设计，通过将数据缓存到访问速度更快的存储设备中，来提高数据的访问速度，如内存、CPU缓存、硬盘缓存等。

但与缓存的高速相对的是，缓存的成本较高，因此容量往往是有限的，当缓存满了之后，就需要一种策略来决定将哪些数据移除出缓存，以腾出空间来存储新的数据。

这样的策略被称为缓存替换策略（Cache Replacement Policy）。

常见的缓存替换策略有：FIFO（First In First Out）、LRU（Least Recently Used）、LFU（Least Frequently Used）等。

核心思想

LRU算法基于这样一个假设：如果数据最近被访问过，那么将来被访问的几率也更高。

大部分情况下这个假设是成立的，因此LRU算法也是比较常用的缓存替换策略。

基于这个假设，我们在实现的时候，需要维护一个有序的数据结构，来记录数据的访问历史，当缓存满了之后，就可以根据这个数据结构来决定将哪些数据移除出缓存。

不适用场景

但如果数据的访问模式不符合LRU算法的假设，那么LRU算法就会失效。

例如：数据的访问模式是周期性的，那么LRU算法就会把周期性的数据淘汰掉，这样就会导致缓存命中率的下降。

换个说法比如，如果现在缓存的数据只在白天被访问，晚上访问的是另一批数据，那么在晚上，LRU算法就会把白天访问的数据淘汰掉，第二天白天又会把昨天晚上访问的数据淘汰掉，这样就会导致缓存命中率的下降。

后面有时间会给大家介绍LFU（Least Frequently Used）算法，以及LFU和LRU的结合LFRU（Least Frequently and Recently Used）算法，可以有效的解决这个问题。

算法基本实现

上文提到，LRU算法需要维护一个有序的数据结构，来记录数据的访问历史。通常我们会用双向链表来实现这个数据结构，因为双向链表可以在O(1)的时间复杂度内往链表的头部或者尾部插入数据，以及在O(1)的时间复杂度内删除数据。

我们将数据存储在双向链表中，每次访问数据的时候，就将数据移动到链表的尾部，这样就可以保证链表的尾部就是最近访问的数据，链表的头部就是最久没有被访问的数据。

当缓存满了之后，如果需要插入新的数据，因为链表的头部就是最久没有被访问的数据，所以我们就可以直接将链表的头部删除，然后将新的数据插入到链表的尾部。

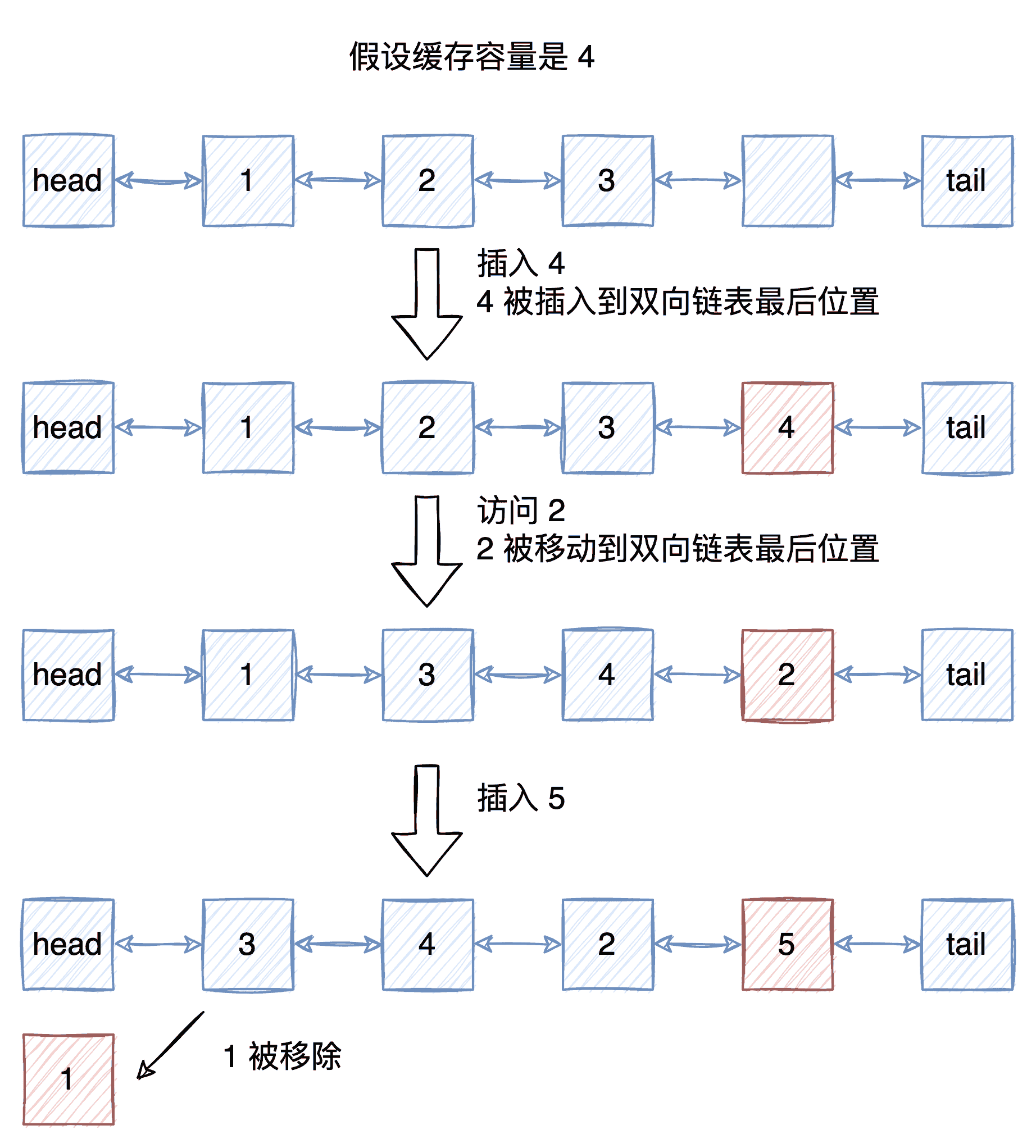
LRU缓存替换策略及C#实现方法是什么

如果我们要实现一个键值对的缓存，我们可以用一个哈希表来存储键值对，这样就可以在O(1)的时间复杂度内完成查找操作，.NET 中我们可以使用 Dictionary。

同时我们使用 LinkedList 来作为双向链表的实现，存储缓存的 key，以此记录数据的访问历史。

我们在每次操作 Dictionary 进行插入、删除、查找的时候，都需要将对应的 key 也插入、删除、移动到链表的尾部。

// 实现 IEnumerable 接口，方便遍历
public class LRUCache<TKey, TValue> : IEnumerable<KeyValuePair<TKey, TValue>>
{
    private readonly LinkedList<TKey> _list;

    private readonly Dictionary<TKey, TValue> _dictionary;

    private readonly int _capacity;
    
    public LRUCache(int capacity)
    {
        _capacity = capacity;
        _list = new LinkedList<TKey>();
        _dictionary = new Dictionary<TKey, TValue>();
    }

    public TValue Get(TKey key)
    {
        if (_dictionary.TryGetValue(key, out var value))
        {
            // 在链表中删除 key，然后将 key 添加到链表的尾部
            // 这样就可以保证链表的尾部就是最近访问的数据，链表的头部就是最久没有被访问的数据
            // 但是在链表中删除 key 的时间复杂度是 O(n)，所以这个算法的时间复杂度是 O(n)
            _list.Remove(key);
            _list.AddLast(key);
            return value;
        }

        return default;
    }

    public void Put(TKey key, TValue value)
    {
        if (_dictionary.TryGetValue(key, out _))
        {
            // 如果插入的 key 已经存在，将 key 对应的值更新，然后将 key 移动到链表的尾部
            _dictionary[key] = value;
            _list.Remove(key);
            _list.AddLast(key);
        }
        else
        {          
            if (_list.Count == _capacity)
            {
                // 缓存满了，删除链表的头部，也就是最久没有被访问的数据
                _dictionary.Remove(_list.First.Value);
                _list.RemoveFirst();
            }

            _list.AddLast(key);
            _dictionary.Add(key, value);
        }
    }

    public void Remove(TKey key)
    {
        if (_dictionary.TryGetValue(key, out _))
        {
            _dictionary.Remove(key);
            _list.Remove(key);
        }
    }

    public IEnumerator<KeyValuePair<TKey, TValue>> GetEnumerator()
    {
        foreach (var key in _list)
        {
            yield return new KeyValuePair<TKey, TValue>(key, _dictionary[key]);
        }
    }

    IEnumerator IEnumerable.GetEnumerator()
    {
        return GetEnumerator();
    }
}
var lruCache = new LRUCache<int, int>(4);

lruCache.Put(1, 1);
lruCache.Put(2, 2);
lruCache.Put(3, 3);
lruCache.Put(4, 4);

Console.WriteLine(string.Join(" ", lruCache));
Console.WriteLine(lruCache.Get(2));
Console.WriteLine(string.Join(" ", lruCache));
lruCache.Put(5, 5);
Console.WriteLine(string.Join(" ", lruCache));
lruCache.Remove(3);
Console.WriteLine(string.Join(" ", lruCache));

输出：

[1, 1] [2, 2] [3, 3] [4, 4] // 初始化
2                           // 访问 2
[1, 1] [3, 3] [4, 4] [2, 2] // 2 移动到链表尾部
[3, 3] [4, 4] [2, 2] [5, 5] // 插入 5
[4, 4] [2, 2] [5, 5]        // 删除 3

算法优化

上面的实现中，对缓存的查询、插入、删除都会涉及到链表中数据的删除（移动也是删除再插入）。

因为我们在 LinkedList 中存储的是 key，所以我们需要先通过 key 在链表中找到对应的节点，然后再进行删除操作，这就导致了链表的删除操作的时间复杂度是 O(n)。

虽然 Dictionary 的查找、插入、删除操作的时间复杂度都是 O(1)，但因为链表操作的时间复杂度是 O(n)，整个算法的最差时间复杂度是 O(n)。

算法优化的关键在于如何降低链表的删除操作的时间复杂度。

优化思路：

在 Dictionary 中存储 key 和 LinkedList 中节点的映射关系 在 LinkedList 的节点中存储 key-value

也就是说，我们让两个本来不相关的数据结构之间产生联系。

不管是在插入、删除、查找缓存的时候，都可以通过这种联系来将时间复杂度降低到 O(1)。

通过 key 在 Dictionary 中找到对应的节点，然后再从 LinkedList 节点中取出 value，时间复杂度是 O(1) LinkedList 删除数据之前，先通过 key 在 Dictionary 中找到对应的节点，然后再删除，这样就可以将链表的删除操作的时间复杂度降低到 O(1) LinkedList 删除头部节点时，因为节点中存储了 key，所以我们可以通过 key 在 Dictionary 中删除对应的节点，时间复杂度是 O(1)

public class LRUCache_V2<TKey, TValue> : IEnumerable<KeyValuePair<TKey, TValue>>
{
    private readonly LinkedList<KeyValuePair<TKey, TValue>> _list;
    
    private readonly Dictionary<TKey, LinkedListNode<KeyValuePair<TKey, TValue>>> _dictionary;
    
    private readonly int _capacity;
    
    public LRUCache_V2(int capacity)
    {
        _capacity = capacity;
        _list = new LinkedList<KeyValuePair<TKey, TValue>>();
        _dictionary = new Dictionary<TKey, LinkedListNode<KeyValuePair<TKey, TValue>>>();
    }
    
    public TValue Get(TKey key)
    {
        if (_dictionary.TryGetValue(key, out var node))
        {
            _list.Remove(node);
            _list.AddLast(node);
            return node.Value.Value;
        }
        
        return default;
    }
    
    public void Put(TKey key, TValue value)
    {
        if (_dictionary.TryGetValue(key, out var node))
        {
            node.Value = new KeyValuePair<TKey, TValue>(key, value);
            _list.Remove(node);
            _list.AddLast(node);
        }
        else
        {
            if (_list.Count == _capacity)
            {
                _dictionary.Remove(_list.First.Value.Key);
                _list.RemoveFirst();
            }
            
            var newNode = new LinkedListNode<KeyValuePair<TKey, TValue>>(new KeyValuePair<TKey, TValue>(key, value));
            _list.AddLast(newNode);
            _dictionary.Add(key, newNode);
        }
    }
    
    public void Remove(TKey key)
    {
        if (_dictionary.TryGetValue(key, out var node))
        {
            _dictionary.Remove(key);
            _list.Remove(node);
        }
    }

    public IEnumerator<KeyValuePair<TKey, TValue>> GetEnumerator()
    {
        return _list.GetEnumerator();
    }

    IEnumerator IEnumerable.GetEnumerator()
    {
        return GetEnumerator();
    }
}

进一步优化

因为我们对 双向链表 的存储需求是定制化的，要求节点中存储 key-value，直接使用 C# 的 LinkedList 我们就需要用 KeyValuePair 这样的结构来间接存储，会导致一些不必要的内存开销。

我们可以自己实现一个双向链表，这样就可以直接在节点中存储 key-value，从而减少内存开销。

public class LRUCache_V3<TKey, TValue>
{
    private readonly DoubleLinkedListNode<TKey, TValue> _head;

    private readonly DoubleLinkedListNode<TKey, TValue> _tail;

    private readonly Dictionary<TKey, DoubleLinkedListNode<TKey, TValue>> _dictionary;

    private readonly int _capacity;

    public LRUCache_V3(int capacity)
    {
        _capacity = capacity;
        _head = new DoubleLinkedListNode<TKey, TValue>();
        _tail = new DoubleLinkedListNode<TKey, TValue>();
        _head.Next = _tail;
        _tail.Previous = _head;
        _dictionary = new Dictionary<TKey, DoubleLinkedListNode<TKey, TValue>>();
    }

    public TValue Get(TKey key)
    {
        if (_dictionary.TryGetValue(key, out var node))
        {
            RemoveNode(node);
            AddLastNode(node);
            return node.Value;
        }

        return default;
    }

    public void Put(TKey key, TValue value)
    {
        if (_dictionary.TryGetValue(key, out var node))
        {
            RemoveNode(node);
            AddLastNode(node);
            node.Value = value;
        }
        else
        {
            if (_dictionary.Count == _capacity)
            {
                var firstNode = RemoveFirstNode();

                _dictionary.Remove(firstNode.Key);
            }

            var newNode = new DoubleLinkedListNode<TKey, TValue>(key, value);
            AddLastNode(newNode);
            _dictionary.Add(key, newNode);
        }
    }

    public void Remove(TKey key)
    {
        if (_dictionary.TryGetValue(key, out var node))
        {
            _dictionary.Remove(key);
            RemoveNode(node);
        }
    }

    private void AddLastNode(DoubleLinkedListNode<TKey, TValue> node)
    {
        node.Previous = _tail.Previous;
        node.Next = _tail;
        _tail.Previous.Next = node;
        _tail.Previous = node;
    }

    private DoubleLinkedListNode<TKey, TValue> RemoveFirstNode()
    {
        var firstNode = _head.Next;
        _head.Next = firstNode.Next;
        firstNode.Next.Previous = _head;
        firstNode.Next = null;
        firstNode.Previous = null;
        return firstNode;
    }

    private void RemoveNode(DoubleLinkedListNode<TKey, TValue> node)
    {
        node.Previous.Next = node.Next;
        node.Next.Previous = node.Previous;
        node.Next = null;
        node.Previous = null;
    }
    
    internal class DoubleLinkedListNode<TKey, TValue>
    {    
        public DoubleLinkedListNode()
        {
        }

        public DoubleLinkedListNode(TKey key, TValue value)
        {
            Key = key;
            Value = value;
        }

        public TKey Key { get; set; }
        
        public TValue Value { get; set; }

        public DoubleLinkedListNode<TKey, TValue> Previous { get; set; }

        public DoubleLinkedListNode<TKey, TValue> Next { get; set; }
    }
}

Benchmark

使用 BenchmarkDotNet 对3个版本进行性能测试对比。

[MemoryDiagnoser]
public class WriteBenchmarks
{
    // 保证写入的数据有一定的重复性，借此来测试LRU的最差时间复杂度
    private const int Capacity = 1000;
    private const int DataSize = 10_0000;
    
    private List<int> _data;

    [GlobalSetup]
    public void Setup()
    {
        _data = new List<int>();
        var shared = Random.Shared;
        for (int i = 0; i < DataSize; i++)
        {
            _data.Add(shared.Next(0, DataSize / 10));
        }
    }
    
    [Benchmark]
    public void LRUCache_V1()
    {
        var cache = new LRUCache<int, int>(Capacity);
        foreach (var item in _data)
        {
            cache.Put(item, item);
        }
    }
    
    [Benchmark]
    public void LRUCache_V2()
    {
        var cache = new LRUCache_V2<int, int>(Capacity);
        foreach (var item in _data)
        {
            cache.Put(item, item);
        }
    }
    
    [Benchmark]
    public void LRUCache_V3()
    {
        var cache = new LRUCache_V3<int, int>(Capacity);
        foreach (var item in _data)
        {
            cache.Put(item, item);
        }
    }
}

public class ReadBenchmarks
{
    // 保证写入的数据有一定的重复性，借此来测试LRU的最差时间复杂度
    private const int Capacity = 1000;
    private const int DataSize = 10_0000;
    
    private List<int> _data;
    private LRUCache<int, int> _cacheV1;
    private LRUCache_V2<int, int> _cacheV2;
    private LRUCache_V3<int, int> _cacheV3;

    [GlobalSetup]
    public void Setup()
    {
        _cacheV1 = new LRUCache<int, int>(Capacity);
        _cacheV2 = new LRUCache_V2<int, int>(Capacity);
        _cacheV3 = new LRUCache_V3<int, int>(Capacity);
        _data = new List<int>();
        var shared = Random.Shared;
        for (int i = 0; i < DataSize; i++)
        {
            int dataToPut  = shared.Next(0, DataSize / 10);
            int dataToGet = shared.Next(0, DataSize / 10);
            _data.Add(dataToGet);
            _cacheV1.Put(dataToPut, dataToPut);
            _cacheV2.Put(dataToPut, dataToPut);
            _cacheV3.Put(dataToPut, dataToPut);
        }
    }
    
    [Benchmark]
    public void LRUCache_V1()
    {
        foreach (var item in _data)
        {
            _cacheV1.Get(item);
        }
    }
    
    [Benchmark]
    public void LRUCache_V2()
    {
        foreach (var item in _data)
        {
            _cacheV2.Get(item);
        }
    }
    
    [Benchmark]
    public void LRUCache_V3()
    {
        foreach (var item in _data)
        {
            _cacheV3.Get(item);
        }
    }
}

写入性能测试结果：

|      Method |      Mean |     Error |    StdDev |    Median |     Gen0 |     Gen1 | Allocated |
|------------ |----------:|----------:|----------:|----------:|---------:|---------:|----------:|
| LRUCache_V1 | 16.890 ms | 0.3344 ms | 0.8012 ms | 16.751 ms | 750.0000 | 218.7500 |   4.65 MB |
| LRUCache_V2 |  7.193 ms | 0.1395 ms | 0.3958 ms |  7.063 ms | 703.1250 | 226.5625 |   4.22 MB |
| LRUCache_V3 |  5.761 ms | 0.1102 ms | 0.1132 ms |  5.742 ms | 585.9375 | 187.5000 |   3.53 MB |

查询性能测试结果：

|      Method |      Mean |     Error |    StdDev |    Gen0 | Allocated |
|------------ |----------:|----------:|----------:|--------:|----------:|
| LRUCache_V1 | 19.475 ms | 0.3824 ms | 0.3390 ms | 62.5000 |  474462 B |
| LRUCache_V2 |  1.994 ms | 0.0273 ms | 0.0242 ms |       - |       4 B |
| LRUCache_V3 |  1.595 ms | 0.0187 ms | 0.0175 ms |       - |       3 B |

以上就是关于“LRU缓存替换策略及C#实现方法是什么”这篇文章的内容，相信大家都有了一定的了解，希望小编分享的内容对大家有帮助，若想了解更多相关的知识内容，请关注捷杰建站行业资讯频道。

原创声明
本站部分文章基于互联网的整理，我们会把真正“有用/优质”的文章整理提供给各位开发者。本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
本文链接：http://www.jiecseo.com/news/show_25066.html
lru

相关新闻

Linux下DedeCMS详细安全设置教程
dedecms 上传目录路径
织梦58织梦模板加固版教程详解
加固版织梦CMS整站源码通用安装教程
织梦安装入门视频教程（织梦58莹莹主讲）
修改dede专题管理功能 自定义节点容器模板
织梦(Dedecms)文档关键词维护,文章页自动添加关键词内链锚文本
dedecms把文章批量设为未审核的办法
使用DEDE织梦计划任务功能定时更新首页

本站采用系统自动发货方式，付款后即出现下载入口，如有疑问请咨询在线客服！

售后时间：早10点 - 晚11:30点

咨询售后客服

推荐模板

推荐精华

热门标签

网站模板 企业网站模板 网站模板下载 简单大气 个人网站模板 手机网站模板 响应式网站模板 门户网站模板 下载免费网站模板 学校网站模板 网站模板免费下载 旅游网站模板 电子商务网站模板 公司网站模板 教育网站模板 外贸网站模板 政府网站模板 新闻网站模板 免费网站模板下载 导航网站模板 音乐网站模板 班级网站模板 传奇网站模板 网站 模板 php个人网站模板 汽车网站模板 html个人网站模板 个人网站模板下载 工艺品网站模板 广告公司网站模板
服务热线 19970861797
服务热线 19970861797服务热线 19970861797
售前咨询
售后客服
立即联系
售前客服
立即联系
售后服务
售后客服
立即联系
投诉电话：19970861797
手机二维码
【捷杰建站】
关于我们| 支付账号| 帮助中心| 客户服务| 售后服务| 网站地图 AI工具箱

Copyright © 2024 jiecseo.com All rights reserved.  粤ICP备18085929号

欢迎光临【捷杰建站】，本站所有资源仅供学习与参考，禁止用于商业用途或从事违法行为！

技术营运：深圳市晟艺互动传媒有限公司