本文小编为大家详细介绍“Python中怎么用scipy生成特殊矩阵”，内容详细，步骤清晰，细节处理妥当，希望这篇“Python中怎么用scipy生成特殊矩阵”文章能帮助大家解决疑惑，下面跟着小编的思路慢慢深入，一起来学习新知识吧。
scipy.linalg中提供了一系列特殊矩阵的生成方法，包括循环矩阵、汉克尔矩阵、费德勒矩阵、阿达马矩阵、莱斯利矩阵、希尔伯特及其逆矩阵、帕斯卡及其逆矩阵等。
A = circulant([1,2,3]) print(A) ''' [[1 3 2] [2 1 3] [3 2 1]] '''
汉克尔矩阵和循环矩阵十分相似，不过在向左移位的过程中，hankel(c, r=None)在末尾直接赋0。若r不为None，则通过r对末位进行赋值
print(hankel([1,2,3,4], [0,7,7,8,9])) ''' [[1 2 3 4 7] [2 3 4 7 7] [3 4 7 7 8] [4 7 7 8 9]] '''
阿达马矩阵的每个元素都是± 1 \\pm1±1，每行都互相正交，常用于纠错码。在scipy.linalg中，hadamard(n, dtype)根据n来生成标准的n × n n\\times nn×n阿达马矩阵，需要注意n nn必须为偶数，dtype为可选参数，用于指明矩阵的数据类型。
print(hadamard(4)) ''' [[ 1 1 1 1] [ 1 -1 1 -1] [ 1 1 -1 -1] [ 1 -1 -1 1]] '''
leslie(f, s)，其输入f ff和s ss两个向量，输出矩阵的形式为
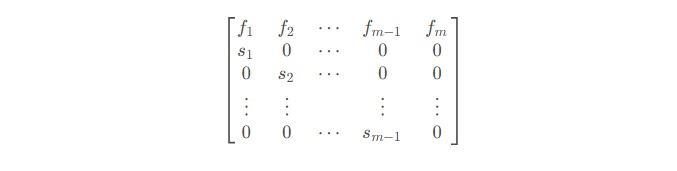
print(leslie([0.1, 2.0, 1.0, 0.1], [0.2, 0.8, 0.7])) ''' [[0.1 2. 1. 0.1] [0.2 0. 0. 0. ] [0. 0.8 0. 0. ] [0. 0. 0.7 0. ]] '''
print(hilbert(3)) ''' [[1. 0.5 0.33333333] [0.5 0.33333333 0.25 ] [0.33333333 0.25 0.2 ]] '''
invhilbert(n, exact=False)可生成n × n n\\times nn×n希尔伯特矩阵的逆矩阵，当exact为False时，返回np.float64类型矩阵；否则返回np.int64类型。
print(pascal(4)) ''' [[ 1 1 1 1] [ 1 2 3 4] [ 1 3 6 10] [ 1 4 10 20]] '''
invpascal可生成逆帕斯卡矩阵，其参数与pascal相同。
读到这里，这篇“Python中怎么用scipy生成特殊矩阵”文章已经介绍完毕，想要掌握这篇文章的知识点还需要大家自己动手实践使用过才能领会，如果想了解更多相关内容的文章，欢迎关注捷杰建站行业资讯频道。
本站采用系统自动发货方式，付款后即出现下载入口，如有疑问请咨询在线客服！
售后时间：早10点 - 晚11:30点
服务热线 19970861797
返回顶部
